| (1) |
Stefan Keller - Yoichi Ito - Kouichi Nishimura1
July 14, 1997
In laboratory environments dense flow avalanches may be investigated as granular flows on inclined chutes. They have the advantage that they can be repeated many times and studied under the same conditions. A disadvantage in the experiment is the difficulty to reproduce the material properties of snow in a dense flow avalanche.
On this subject, different experiments with different materials have been carried out. E.g., in Plüss (1987), using plastic beads, in Kosugi et al. (1995), with ping pong balls, and in Nohguchi (1997), with styrene foam particles; in all of these measurements the main focus was in the flow propagation and related aspects. In another group of experiments, the main investigation was the measurement of velocity profiles in the flow. There are, e.g., the review of Savage et al. (1983), Hungr and Morgenstern (1984), Drake (1990) and Nishimura (1990) and Nishimura et al. (1993). In all these experiments, different materials (mostly spheres) and bed roughness have been used, common is the velocity measurement in the body of quasi two-dimensional flows through transparent side walls.
In this paper, large scale experiments with ping pong ball (PPB) flows in a channeled and open setup are described, the focus here lies on the velocity distribution (of particle and air) in the flow. For the particle velocity measurement, a vertically placed video camera is used. This allows a remote measurement in the centre of the flow, without any influence of side walls. The air velocity within the flow is measured on the basis of static pressure depression. The main investigation is the study of the distinct head-tail structure, which is inherent of most granular flows and snow avalanches. These measurements are part of a project investigating the dynamics and internal structures of snow avalanches, including systematic observations of real avalanches in Kurobe Canyon (Japan) and artificially released snow flows on a ski jump field. The most recent results are summarized in Nishimura et al. (1997).
The similarity of granular flows is mainly governed by the following set of
physical parameters (from Hutter 1984):
| (1) |
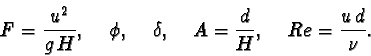 |
(2) |
Nohguchi (1997), on the other hand, describes a similarity analysis for the formation of a head-tail structure in granular flows, which depends on the terminal velocity of the flow and on the slope length. This similarity is valid for granular flows with PPB as well as for snow avalanches.
In addition it can be mentioned, that PPB flows fulfill the condition of easily being calculated, since there is no cohesion between the balls. This is very ideal for the application of the, e.g., Savage-Hutter model (Savage and Hutter, 1989), currently the most complex model for granular flows that is being used to model snow avalanches.
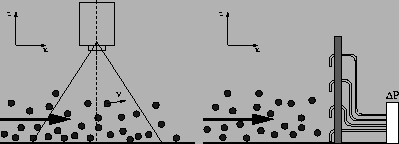
The channeled flows were carried out in the chute of the Shinjo
branch of Snow and Ice studies, NIED, Japan. The chute
has a slope angle of 30![]() and a width of
1m. The ground and one side wall consist of glass plates, while the
other side wall is made of wood. The balls were kept in a container on the
top of the chute. The velocity measurement was
made after a runout distance of 14.5m, in the center of the chute.
and a width of
1m. The ground and one side wall consist of glass plates, while the
other side wall is made of wood. The balls were kept in a container on the
top of the chute. The velocity measurement was
made after a runout distance of 14.5m, in the center of the chute.
The three-dimensional experiments
were made at the Miyanomori 70m ski jump field in Sapporo.
The ground consists of plastic wires (artificial grass for ski jumpers).
The balls were
put into a large box just below the edge of the jump field, from where
the flow could develop over the landing track.
After a flow distance of 55m the steepest slope
angle of 36![]() is reached (where the avalanches were in a
steady state condition), at a
distance of 85m the measurement devices were installed: the video
camera for the measurement of the particle velocities on the left side,
2.4m from the flow center, and the tubes for the air flow measurement on the
right side, 1.5m from the flow centre.
is reached (where the avalanches were in a
steady state condition), at a
distance of 85m the measurement devices were installed: the video
camera for the measurement of the particle velocities on the left side,
2.4m from the flow center, and the tubes for the air flow measurement on the
right side, 1.5m from the flow centre.
In all experiments ping pong balls with a diameter of 37.7mm and
a weight of 2.48g (![]() = 0.0884gcm-1)
were used. The free falling velocity
is calculated to be 9.4ms-1.
In the chute, avalanches with 2000, 3000 and
6000 balls, in the three-dimensional setup, with 150,000,
200,000 and 300,000 balls were produced (see figure 1).
= 0.0884gcm-1)
were used. The free falling velocity
is calculated to be 9.4ms-1.
In the chute, avalanches with 2000, 3000 and
6000 balls, in the three-dimensional setup, with 150,000,
200,000 and 300,000 balls were produced (see figure 1).
The velocity measurement of the PPBs is based on the uniform ball size: balls close to the observer, a video camera e.g., appear bigger than balls further away (figure 2). I.e., with the visible diameter of a ball in the picture frame of the video camera, the location of the ball, including the distance from the camera, can be calculated. If the same ball can be tracked within two subsequent pictures, the three-dimensional velocity vector is obtained. In the calculation, different corrections have to be included, such as the distortion of the lens system and rotation and position of the camera to the ground. For this measurements an ordinary video camera with a wide angle lens was used. The height over the ground of the camera was fixed at 470mm and 820mm, in the channeled and in the open flow, respectively. For the evaluation of the coordinates and the calculation of the velocities, the maximum resolution of 60 pictures in a second, which are stored on the video tape, was used.
The accuracy strongly depends on the distance of the ball
from the camera; at 450mm, the error in the calculation of the
distance is about ![]() 25mm, at 800mm, it is
increased to
25mm, at 800mm, it is
increased to ![]() 80mm. The error in the horizontal coordinate
is smaller: the accuracy of the down slope velocity component is
about 5% at a distance of 450mm and a ball velocity of 8ms-1, and
about 8% at a distance of 800mm and a ball velocity of 15ms-1.
80mm. The error in the horizontal coordinate
is smaller: the accuracy of the down slope velocity component is
about 5% at a distance of 450mm and a ball velocity of 8ms-1, and
about 8% at a distance of 800mm and a ball velocity of 15ms-1.
To calculate the velocity, a ball has to be seen in two subsequent frames. In the head of dense flows, the density is often so high, that only balls from the upper part can be measured.
For this purpose, four tubes were fixed at 0.01, 0.15, 0.3 and 0.45m
above the ground, with the open ends looking downwards
(figure 2). The inner diameter
of a tube is 10mm, the length is 35m, the ends are connected with
sensitive pressure difference sensors. The air flow
perpendicular to the
tube induces a reduced pressure in the tube. For a downslope velocity u
the pressure difference ![]() is
is
| (3) |
Characteristics that distingish head and tail are ball velocity and flow height. Figure 3 shows the maximum velocities, umax (average of the three highest values in the main flow direction) and the flow height (centre of ball). In the latter, the highest ball has been excluded, assuming being an isolated jumping ball. The flow height shows clearly the shape of the avalanche head, which is about twice as high as the following tail. A similar tendency can be seen in the velocities. They increase first to a maximum value within the avalanche head, and then decrease slightly in the tail. From now on, the head shall be defined as the first part of the flow with the high flow height. For the avalanches in the chute, this corresponds up to 233, 283 and 317ms (2000, 3000 and 6000 balls, respectively).
The measured front velocities ufr of the flows are:
6.3, 6.3 and 6.8ms-1 (for 2000, 3000 and 6000 balls,
respectively). This gives the following ratios of the maximum velocity to
the front velocity
umax/ufr: 1.4, 1.43 and 1.35.
Thus, a mean ratio
![]() can be assumed.
can be assumed.
Figure 4 is a representation of vertical profiles in the head of the avalanche with 3000 balls. In each profile, the start and end points of the balls after a time interval of 17ms are given. It can be seen, that the vertical activity is high; the balls are jumping up and down.
Averaged vertical profiles of the downslope velocity components
in the rear part of the head (117 - 167ms, where
![]() const.) and tail are given in
figure 5. In the head, the vertical profiles show
lower velocities at the ground, the balls in the middle part
of the flow and towards the surface are
const.) and tail are given in
figure 5. In the head, the vertical profiles show
lower velocities at the ground, the balls in the middle part
of the flow and towards the surface are ![]() 1ms-1 faster. In the
tail, this is very different: the profiles are almost constant and no
reduced velocities at the ground can be seen.
The mean flow heights in the tail are 70, 70 and 90mm, corresponding
to about 2.5, 2.5 and 3 layers of balls.
Since there are few jumping balls, the flow heights in figure 3
appear to be bigger.
The lateral profiles in head and
tail are constant. The lateral component of the velocities v is
small anyway, it is
1ms-1 faster. In the
tail, this is very different: the profiles are almost constant and no
reduced velocities at the ground can be seen.
The mean flow heights in the tail are 70, 70 and 90mm, corresponding
to about 2.5, 2.5 and 3 layers of balls.
Since there are few jumping balls, the flow heights in figure 3
appear to be bigger.
The lateral profiles in head and
tail are constant. The lateral component of the velocities v is
small anyway, it is
![]() at any time and at all
avalanche sizes in the chute.
at any time and at all
avalanche sizes in the chute.
The volume fraction cball of the balls in the
flow was not measured directly. Estimations give
![]() in the lower parts of the head, which decreases to
in the lower parts of the head, which decreases to
![]() in the tail.
in the tail.
Another difference between head and tail follows from the fluctuations
of the different velocity components. The mean standard deviations
![]() ,
,
![]() and
and
![]() (which is the square root
of the granular temperature, as it is introduced by Ogawa (1978)),
calculated from the velocities at each time step, and then averaged over
the head and the tail, are
given in table 1.
The fluctuations are always higher in the head than in the tail.
(which is the square root
of the granular temperature, as it is introduced by Ogawa (1978)),
calculated from the velocities at each time step, and then averaged over
the head and the tail, are
given in table 1.
The fluctuations are always higher in the head than in the tail.
The same representations of the maximum downslope velocities and flow heights with time for the unconfined flows at the Miyanomori ski jump are given in figure 6. The curves are no longer similar for the different flow sizes. This corresponds to the varying flow pattern in the open runout (see also figure 1). For the smallest avalanche for example, the position of the video camera was near the edge of the flow, where the head is relatively long. This situation has an influence on the ratio of the maximum velocity in the flow, umaxto the front velocity ufr: for the 150,000 ball avalanche, umax/ufr = 1.15, while for the bigger avalanches it is 1.25 and 1.23 (the front velocities are 13.6, 13.6 and 15.0ms-1, respectively).
Figure 7 shows vertical and lateral profiles in the head of the avalanche with 200,000 balls. The time interval of one profile is 17ms. Again there is high vertical activity. The lateral profiles show during the first 50ms (corresponding to a length of about 0.7m) a strong movement outwards, away from the centre of the flow (which is at y = - 2.4m). After this first part in the head, there is not anymore a specific lateral movement. Further behind the head (from 133 - 167ms) the lateral profiles are not uniform; the balls with low y-values, towards the centre of the flow, are faster. Towards the tail (from 183ms on), this tendency can not be recognized anymore; there, the flow seems to be uniform, without any specific lateral velocity component. As in the channeled flows, the vertical profiles in the tail (figure 8) are almost constant. The mean flow heights in the tail are 100, 120 and 140mm, corresponding to about 3, 3.5 and 4 layers of balls.
Again, the fluctuations of the different velocity components in the head are higher than in the tail (table 2).
All results listed above describe characterizations of the balls in the avalanche. With the measurement of the static pressure depression, characteristics of the air flow around the balls and above the flow can be obtained. In figure 8, mean velocities in the tail are given. The vertical profiles are more or less uniform. Remarkably, there are no reduced air velocities above the flows. The second sensor at a height of 150mm is at the surface of the tail of the PPB flow, above there are only jumping balls. But the flow induced air movement can be seen even 300 - 350mm above the flow surface and 250 - 300mm above the highest jumping balls.
In ping pong ball avalanches as in other similar flows the formation of a head is very obvious, something which does not occur in flows with golf balls, for example. From the results, the head and tail are distinguished in many ways, which is summarized in the following. Most remarkably is height, which is more than twice as high in the head as in the tail. The downslope velocity arises to its maximum in the head, while it is a bit lower in the tail. Only in the head is there an influence of the ground friction. The fluctuations of all velocity components are higher in the head than in the tail. All this comes together with higher ball concentrations in the head. Since the maximum flow velocity is in the head and not in the tail, there is no feeding of new balls from the rear part of the flow to the front. This is a general occurrence in such a short gravity current.
The different vertical velocity profiles in head and tail are very interesting. This may be explained with the low concentration in the tail. There are less contacts from ball to ball than in the dense head. This allows a longer free length until the next ball contact. As a result, the momentum in the tail is distributed throughout the whole flow height. This is not possible in the dense head; the momentum can not be transferred immediately from the bottom to the top and vice versa.
Comparing these velocity profiles with the above mentioned measurements in other granular flows, the nearly vertical profile is striking, whereas in other flows the balls at the ground are much slower. Although all these measurements vary in many aspects (such as diameter, density, volume fraction, elasticity, restitution and angle of friction of particles, acceleration or steady state of flow), two points seem to be important: the ratio A = d/H, which is comparatively high in the present experiments, and the roughness, which is very low.
The comparison of the obtained velocity profiles with the few available measurements in dense flow avalanches in nature (Gubler, 1987, Dent et al., 1994) point out a different behaviour at the bottom of the flows. While in nature at the ground a high velocity gradient and therefore high shear stress is measured, there is nothing similar to see in the PPB avalanches. Above this zone of high velocity gradients, all profiles are similar, showing roughly constant velocities. There are different material properties, ground friction etc, which explain the different flow structures near the ground. However, in spite of the different properties, in the upper flow part, the profiles are similar.
The higher fluctuation of the downslope velocity in the head partly follows from the vertical velocity gradient, since the fluctuation was calculated from the mean velocity of all measured balls at the same time. But the higher fluctuations of the other velocity components, where no distinct velocity gradient is measured, show, that there are in general increased activities in the head.
The ratio of maximum velocity to front velocity
umax/ufr in
the open flow is lower than in the chute. It can be seen, that the
velocities in the centre of the flow are higher, so that the same
ratio
![]() may be
reached, as observed in the chute.
As a comparison: in powder snow avalanches experiments in
the laboratory (Keller, 1996),
with small glass spheres as the particle phase and water as
the fluid phase, a constant ratio
umax/ufr = 1.5 has been found,
independent on the initial particle volume, distance in the runout zone
and slope angle. Further measurements with ping pong balls have to
prove, whether the velocity ratio in PPB flows shows the same behaviour.
may be
reached, as observed in the chute.
As a comparison: in powder snow avalanches experiments in
the laboratory (Keller, 1996),
with small glass spheres as the particle phase and water as
the fluid phase, a constant ratio
umax/ufr = 1.5 has been found,
independent on the initial particle volume, distance in the runout zone
and slope angle. Further measurements with ping pong balls have to
prove, whether the velocity ratio in PPB flows shows the same behaviour.
The PPB avalanches in the chute have a very small lateral velocity component, and it has been shown, that the influence of the side walls to the velocity distribution is below the accuracy of the measurement. Thus, such a channeled avalanche can really be regarded as a two-dimensional flow. This is different to the open flow on the ski jump field. The head shows rather a complex structure, with a short time of 0.05s (which corresponds to a flow length of approx. 0.7m), where the velocity is directed outwards of the main flow direction. In the same time, the velocity increases, followed by a short period (roughly 0.08s), where the downslope velocities of the balls closer to the middle of the flow are slightly higher. Afterwards, in the rear part of the head and in the tail, the flow is uniform and can be regarded as two-dimensional.
The measurement of the air velocity in and above the tail shows high, flow induced velocities distinctly above the flow surface. A possible explanation is that the high avalanche head accelerates all the air mass up to the height of the head and higher, and after decreasing of the avalanche height, the air in the upper parts keeps moving; at least some meters behind the head, where the air flow was measured. With this strong air flow clearly above the flow, it can be understand, why the highest jumping PPBs in the tail do not show any reduced velocity due to air friction; they move within the accelerated air.
The described method for the remote measurement of the location and velocity of a ball with a video camera is an appropriate way for such flows. However, this method is restricted to flows with spheres of uniform sizes or with easy distinguishable different diameters. The accuracy of the distance measurement is restricted to the pixel resolution of the video camera and the quality of the data recording system.
The measurement of the air velocity on the basis of the static pressure depression seems to be an useful way for two phase flows, where other system such as wind anemometer don't work anymore. But it is a serious deficiency that the flow direction, which can not be measured with a single tube, has a strong influence to the pressure depression. An improvement of the system, which is currently applied to new measurements, is the use of different orientated tubes at the same point.
It has been shown that large scale experiments with ping pong ball avalanches allow the study of specific features of granular flows, which help for a better understanding of dense flow avalanches. Different aspects of the head-tail structure, which is a typical property of many granular flows, including snow avalanches, are pointed out. The measurements show that, in the present setup with a smooth surface, there is almost only slip at the ground. A dependance of the shear flow on the ratio A = d/H (particle diameter/flow depth) in the ping pong balls flows can be assumed, in comparison to other measurements, this ratio seems to be at the upper limit.
In future experiments, it might be useful to include different bed roughness, and the dependance of shear flow and vertical velocity profiles on the flow height should be studied.
The authors gratefully acknowledge all the people who joined our experiments in Shinjo and at the ski jump in Sapporo and who contributed in many different ways. This work was enabled by the Japanese Society for the Promotion of Science (JSPS), and the experiments were partly supported by the Grant-in-Aid for Co-operative Research and Science Research of the Ministery of Education, Science and Culture, Japan.
Dent, J.D., E.E. Adams, I.J. Bailey, T.G. Jazbutis and D.S. Schmidt. 1995. Velocity and mass transport measurements in a snow avalanche. In ISSW'94, International Snow Science Workshop, 30 October - 3 November 1994, Snowbird, Utah. Proceedings. Snowbird, UT, P.O. Box 49, 636-642.
Drake, T.G. 1990. Structural features in granular flows.
J. Geophysical Research, 95, no. B6, 8681-8696.
Gubler, H. 1997. Measurements and modelling of snow avalanche speeds.
IAHS Publication 162 (Symposium at Davos 1986 -
Avalanche Formation, Movement and Effects, 405-420.
Hungr, O. and Morgenstern, N.R. 1984. Experiments on the flow behaviour
of granular materials at high velocity in an open channel.
Géotechnique 34, no. 3, 405-413.
Hutter, K. 1994. Avalanche dynamics. In V.P. Singh (Ed.),
Hydrology of Disasters, Kluwer Academic Publishers, chapt. 11, 317-394.
Keller, S. 1996.
Physikalische Simulation von Staublawinen, Experimente zur
Dynamik im dreidimensionalen Auslauf. Eidg. Techn. Hochschule, Zürich.
Versuchsanst. Wasserbau, Hydrol.
Glaziol. Mitt. 141.
Kosugi, K., A. Sato, O. Abe, Y. Nohguchi, Y. Yamada, K. Nishimura and
K. Izumi. 1994. Table tennis ball avalanche experiments. In
ISSW'94, International Workshop, 30 October - 3 November 1994, Snowbird,
Uta. Proceedings. Snowbird, UT, P.O. Box 49, 636-642.
Nishimura, K. 1990. Studies on the fluidized snow dynamics.
Contributions from the Institute of Low Temperature Science, serie A,
no. 37, Hokkaido University, Sapporo, Japan.
Nishimura, K., K. Kosugi and M. Nakagawa. 1993. Experiments
on ice-sphere flows along an inclined chute. Mech. Mat., 16,
205-209.
Nishimura, K., Y. Nohguchi, Y. Ito and K. Kosugi. 1997. Snow
avalanche experiments at ski jump.
In ISSW'96, International Snow Science Workshop,
6-10 October 1996, Banff, Alberta. Proceedings.
Revelstoke, B.C., Canadadian Avalanche Association, 244-251.
Nohguchi, Y. 1997. Avalanche experiments with styrene foam particles.
Snow Engineering: Recent Advances (Proc. 3rd International Conference
on Snow Engineering, 26-31 May 1996,
Sendai, Japan). Izumi, Nakamura & Sack (eds),
Balkema, Rotterdam, 63-68.
Ogawa, S. 1978. Multitemperature theory of granular materials.
In US-Jpn. Semin. Contin.-Mech. and Stat. Approaches
Mech. Granular Mater. Proceedings.
Tokyo: Gukujutsu Bunken Fukyukai, 208-217.
Plüss, Ch. 1987. Experiments on granular avalanches (in german)
Diplomarbeit,
Abt. X, Eidg. Techn. Hochschule Zürich, 113 p.
Savage, S.B. and Hutter, K. 1989. The motion of a finite mass of granular
material down a rough incline. Fluid Meach., 199, 177-215.
Savage, S.B., Nedderman, R.M., Tüzün, U. and Houlsby, G.T. 1983.
The flow of granular materials - III, rapid shear flows.
Chem. Engineering Science, 38, no. 2, 189-195.
| |||||||||||||||||||||||||||||||||||
 |
 |
![\begin{figure}\par\begin{center}
\makebox[100mm][c]{
\begin{picture}
(170,80)
\...
...1,11){\rotatebox{90}{flow height [mm]} }
\end{picture}}
\end{center}\end{figure}](img23.gif) |
![\begin{figure}\par\begin{center}
\makebox[85mm][c]{
\begin{picture}
(85,40)
\pu...
...put(43,13){\rotatebox{90}{height [mm]} }
\end{picture}}
\end{center}\end{figure}](img25.gif) |
![\begin{figure}\par\begin{center}
\makebox[100mm][c]{
\begin{picture}
(170,80)
\...
...1,11){\rotatebox{90}{flow height [mm]} }
\end{picture}}
\end{center}\end{figure}](img23.gif) |
![\begin{figure}\par\begin{center}
\makebox[100mm][c]{
\begin{picture}
(170,80)
\...
... }
\put(0.5,17){\rotatebox{90}{y [mm]} }
\end{picture}}
\end{center}\end{figure}](img26.gif) |
![\begin{figure}\par\begin{center}
\makebox[85mm][c]{
\begin{picture}
(85,40)
\pu...
...put(43,13){\rotatebox{90}{height [mm]} }
\end{picture}}
\end{center}\end{figure}](img25.gif) |
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 chamall.tex.
The translation was initiated by Jim McElwaine on 1999-10-27