![\includegraphics[width=120mm]{BILDER/resolution.eps}](img12.gif)
|
Stefan Keller
Institute of Low Temperature Science
Hokkaido University, Sapporo, Japan
Date: 8, August 1996
The video camera is set perpendicular to the ground. The measurement principle is as follows: The balls close to the lens of the camera appear bigger than those which are further away. Because all balls in one flow have an uniform diameter, the distance from the camera to a ball can be calculated by measuring the size of a ball in the video picture. In the same way, by measuring the distance the ball moves within a certain time, the velocity of the ball can be calculated. Not only the two dimensional velocity vector, parallel to the ground, can be calculated, but also the component in the z-direction, by taking into account the different ball heights before and after this time interval. This time can either be the time interval of two successive frames, ti (``two picture measurement''), or the time of the shutter speed, ts (``one picture measurement''). In the first case, the ball must be seen in both frames, in the second one, the entire path of the ball, looking as a long, rather faint line of the width of one ball diameter must be recognized and measured.
The height hcam of the camera (resp. lens) over the ground is dependent on the opening angle of the camera lens, on the maximum ball velocity vmax, the maximum flow height hmax and the principle of measurement (one or two picture measurement). In order to get a reasonable resolution of the ball height, the camera should be very close to the flow (see figure 1).
![\includegraphics[width=120mm]{BILDER/resolution.eps}](img12.gif)
|
A drawing of the setup with some basic notations can be seen in figure 2.
db diameter of ball,These notations are related to a camera, which is fixed perpendicular to the ground, with the long frame side in the flow direction. However, there might be the situation, that it is not possible to fix it in that way, either that the camera axis is not vertical to the ground or the orientation of the camera frame is not parallel to the flow direction. This has to be taken into account by the evaluation.
zb height over ground of ball,
velocity of ball at height z over ground,
u velocity component in flow direction (x),
v velocity component in y - direction,
w vertical velocity component (z - direction),
umax maximum velocity of ball, in flow direction,
hmax maximum flow height,
hlen distance ground - lens,
dlb = hlen - hb, distance lens - ball,
dmin = hlen - hmax, minimum distance lens - maximum flow height,
m, b geometrical characteristics of lenses,
l(dlb), length of representation at distance dlb,
lmin minimum required length of representation at maximum flow height hmax
(dependent of vmax and principle of measurement),
ti frame interval of camera,
ts shutter speed of camera,
pmax number of pixels in the length side of the video frame,
p(dlb) frame fraction (from length side) of ball at distance dlb from lens.
The coordinate system of the camera frame in pixels (let's say px-py - plane or p-plane with p(px,py) as a point on it) shall be defined with zero in the centre of the frame with the two axis px and py parallel to the edges, with px somewhat in the in main flow direction, i.e., along the long side of the frame (figure 3).
![\includegraphics[width=50mm]{BILDER/pxpyplane.eps}](img16.gif) |
![\includegraphics[width=50mm]{BILDER/xcyczcspace.eps}](img17.gif) |
The calibration includes two parts: The properties of the lens system at the used focal distance with the distortion towards the corners of the frame, and secondly the setup of the camera within the system of the experiment. The first part can be made in the laboratory, and is valid as long as the lens system is unchanged and a constant focal distance is used. The second calibration has to be made at each new experimentel setup, in order to get the orientation of the camera.
For the calibration of the lens system (at a fixed setting) two mappings are necessary:
The calibration of the distortion, fdt, can be made with a grid, which is fixed some distance away from the lens. This grid must be positioned vertical to the axis of the lens. This can be easily made by using a mirror, parallel on the plate with the grid. The camera is now fixed in a position, where the mirror image of the lens is exact in the middle of the whole frame. The orientation and the origin of the grid coordinates must be the same as on the p- and t-plane The pixelcoordinates of different points of the grid can be determined (p-plane, figure 5). Either one can find a closed solution for the mapping fdt, or a grid mapping and interpolation can be used.
The latter may look like the follows: In the p-plane, the coordinates of the points of intersections of the grid lines are measured (such as point p in figure 5). These points can be easily mapped to the t-plane by making the lines parallel and vertical (in the figure, point p is mapped to t). To get the mapping fdt(m(p)) = m(t)of any measurement point m(p) in the p-plane, the grid field, where m(p) is located is searched. The coordinates of the corners of the field are known in the t-plane, therefore, m(t) can be determined by keeping the same location within the the grid field, now in the t-plane.
![\includegraphics[width=60mm]{BILDER/distortion.eps}](img22.gif) |
![\includegraphics[width=60mm]{BILDER/lineardist.eps}](img23.gif) |
The location within the grid can be calculated like the following,
assuming straight grid lines (see figure 6;
actually, they are bent): The line
![]() goes through
M(p) in a way, that
goes through
M(p) in a way, that
![]() .
For the ratio
.
For the ratio
![]() on the analogous line between
on the analogous line between
![]() and
and
![]() ,
the same ratio is valid:
,
the same ratio is valid:
![]() .
Thus, calculating this ratio, it
can be used in the t-frame to calculate M(t).
.
Thus, calculating this ratio, it
can be used in the t-frame to calculate M(t).
A more accurate method uses a two-dimensional spline interpolation, which is carried out from the rectangular t-frame to the distorted p-frame. With an iteration, f-1dt(m(t)) comes as close to m(p), the starting value, as wished.
![\includegraphics[width=105mm]{BILDER/camerasyst.eps}](img30.gif) |
The calibration of the focus distance, i.e., of the mapping
ffoc:
![]() ,
can be made with a length scale, fixed at
different distances from the lens, vertical to the lens axis in the
middle of the frame, in the direction of the tx-axis. Here, the
same grid as above can be used, but only the scale in one direction
is of importance. At a distance D from the lens, the newpixels T
of the length L on the scale are measured. At another distance D2,
the newpixels Tm of the length Lm are measured
(see figure 7).
To get same value T in newpixels at both distances D and D2, it is
,
can be made with a length scale, fixed at
different distances from the lens, vertical to the lens axis in the
middle of the frame, in the direction of the tx-axis. Here, the
same grid as above can be used, but only the scale in one direction
is of importance. At a distance D from the lens, the newpixels T
of the length L on the scale are measured. At another distance D2,
the newpixels Tm of the length Lm are measured
(see figure 7).
To get same value T in newpixels at both distances D and D2, it is
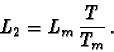 |
(1) |
 |
(2) |
| (4) |
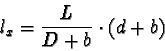 |
(5) |
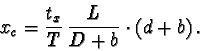 |
(6) |
Therefore, the mapping ffoc:
![]() of a point
a(tx, ty)
in the t-plane with a distance d from the lens is given with
of a point
a(tx, ty)
in the t-plane with a distance d from the lens is given with
Two remarks can be added:
This calibration has to be made at each experiment, where
the camera is new installed or their position is changed. The procedure is
as follows: A scale is fixed at the ground, the direction is the
main flow direction and defines the x-axis of the x-space. The scale
must go through the point, where the vertical line to the focus of the
camera meets the ground plane (V). Again, this can be easily fixed
with a mirror, as stated above. Beside of the point V (see
figures 8 and 9), two other points
on the scale, towards both sides of the frame, shall be fixed while looking
through the camera. Their names shall be A and B and the measured
distance
![]() is
is ![]() (
(![]() remains constant
in the x- and c-space). In the pixelframe,
the p-plane, the corresponding coordinates pV, pA and pB
can be determined.
remains constant
in the x- and c-space). In the pixelframe,
the p-plane, the corresponding coordinates pV, pA and pB
can be determined.
The aim of this calibration is now to define the mapping from the c-space to the x-space. This includes the determination of the vertical distance hf from the focus to the ground plane and the different rotation angles. In the case that the axis of the lens of the camera is fixed perpendicular to the ground and the x-axis of the p-, resp. t-plane and the c-space is in the direction of the main flow, no rotation to the x-space occurs and only the vertical distance hf has to be determined.
The procedure looks like the following. The points pV, pA and pB
are measured in the p-plane. With the mapping fdt:
![]() we get tV, tA and tB, all points should be on one line yet.
The following mapping ffoc:
we get tV, tA and tB, all points should be on one line yet.
The following mapping ffoc:
![]() for these points
can not be calculated, as long as the distances hV,
hA and hB
are not known (see figure 9).
Let's imagine a rotation of the x-space around the
y-axis of the c-space, the rotation angle
for these points
can not be calculated, as long as the distances hV,
hA and hB
are not known (see figure 9).
Let's imagine a rotation of the x-space around the
y-axis of the c-space, the rotation angle
![]() is given in way, that the new x-coordinate of the point V is 0. This
rotation is only related the the x-coordinates and leaves the y-values
unchanged.
is given in way, that the new x-coordinate of the point V is 0. This
rotation is only related the the x-coordinates and leaves the y-values
unchanged.
![\includegraphics[width=90mm]{BILDER/camposground.eps}](img47.gif) |
![\includegraphics[width=105mm]{BILDER/camposside.eps}](img48.gif) |
![\includegraphics[width=83mm]{BILDER/vrotation.eps}](img49.gif) |
![\includegraphics[width=105mm]{BILDER/protation.eps}](img50.gif) |
For the point V, following the mapping from t to c
(equation 10), it is
| (15) |
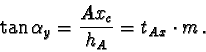 |
(16) |
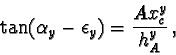 |
(17) |
| (18) |
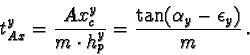 |
(20) |
The next step is the analogous rotation around the x-axis of the c-space.
This rotation angle
![]() is given with the condition, that the
new y-coordinate of V is 0. This rotation affects only y-values.
Again it is
is given with the condition, that the
new y-coordinate of V is 0. This rotation affects only y-values.
Again it is
| (23) |
| hV2 | = | 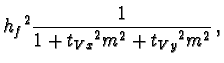 |
(25) |
| dVy2 | = | 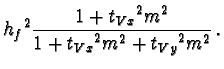 |
(26) |
| (28) |
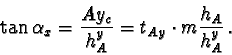 |
(29) |
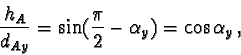 |
(30) |
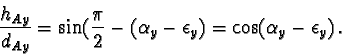 |
(31) |
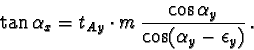 |
(32) |
With these two rotations around the y- and the x-axis of the c-space
and with the angles
![]() and
and
![]() ,
given in
equations 14 and 27, the
ground plane with V is now parallel to the x-y-plane of the c-space.
But the distance hf from the ground plane to the focus is not known yet.
,
given in
equations 14 and 27, the
ground plane with V is now parallel to the x-y-plane of the c-space.
But the distance hf from the ground plane to the focus is not known yet.
hf is related to the measured length
![]() .
In newpixel units, the length is
.
In newpixel units, the length is
![]() ,
with
equations 10 and 11 it is
with
tAxn = tAxy and
tBxn = tBxy:
,
with
equations 10 and 11 it is
with
tAxn = tAxy and
tBxn = tBxy:
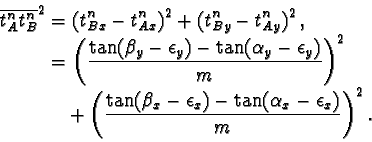 |
(38) |
Here, all angles are defined by the newpixel units of V, A and B, and, therefore, the whole system is determined.
The final step is a rotation around the z-axis of the c-space in order
to get the angle
![]() of the flow direction (given with
of the flow direction (given with
![]() )
to the
x-axis of the c-space.
Because
Vxc = Vyc = 0,
)
to the
x-axis of the c-space.
Because
Vxc = Vyc = 0,
![]() is only dependend on A (or B):
is only dependend on A (or B):
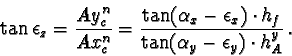 |
(39) |
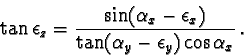 |
(40) |
The same calculation can be made for the situation, where V is not situated on the straight line AB. This is even more conveniant for the procedure of the calibration.
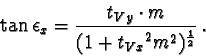
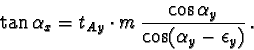
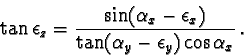
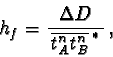
This mapping consists of the three rotations around the axes of the
c-space, the system of the camera, and a shifting along the
x-axis of the x-space. Special attention has to be made at the
definitions of the angles and the directions of the rotations.
It follows,
that the necessary rotations around the x-axis and the z-axis
are opposite
to the definitions of
![]() and
and
![]() .
In the following
calculation, the correct directions of this angles are already assumed,
i.e., the rotations are always in the positive direction.
.
In the following
calculation, the correct directions of this angles are already assumed,
i.e., the rotations are always in the positive direction.
The point in the c-space shall be
![]() .
The first step is
a rotation around the y-axis, with the angle
.
The first step is
a rotation around the y-axis, with the angle
![]() ,
the value
of yc remains untouched. The rotation is given with
,
the value
of yc remains untouched. The rotation is given with
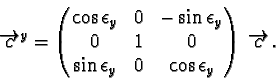 |
(41) |
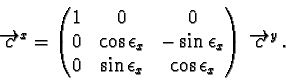 |
(42) |
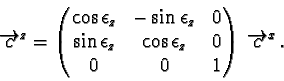 |
(43) |
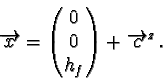 |
(44) |
In the p-frame, the diameter of the ball is measured using two
end points of a diameter in any orientation, D1 and D2. The basic
procedure is as the following, but additionally, it needs a correction
for the real ball diameter and a correction for the real visibility
of the ball.
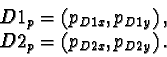 |
(48) |
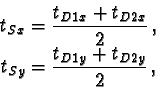 |
(49) |
| (50) |
Actually, the above mentioned calculation is only valid for a ball diameter,
which is measured vertical to the line connecting the centre of the ball
with the origin of the p- and t-frame. In all the other situations,
the ball diameter appears too big and finally it results a too close distance
to the camera. The cause of this error can be understand with
figure 12: What should be measured is the real diameter of
the ball,
![]() .
Actually, a projection
.
Actually, a projection
![]() to a ground plane G, which is parallel to the t-frame and which shall be
defined to go through the centre of the ball, is measured. In the
situation, where the diameter points D1r and D2r have the same distance
from the camera, i.e., the diameter is parallel to G (and is on this
ground plane, actually), D1 and D1r are congruent.
to a ground plane G, which is parallel to the t-frame and which shall be
defined to go through the centre of the ball, is measured. In the
situation, where the diameter points D1r and D2r have the same distance
from the camera, i.e., the diameter is parallel to G (and is on this
ground plane, actually), D1 and D1r are congruent.
In the figure (see as well figure 13), beside the mentioned ground plane G, two more planes are used: The D-plane, connecting the origin with the two diameter points D1 and D2, and the V-plane, which goes through the centre of the ball, C, and which is vertical to co, the line from the origin to C. dg is the intersection line between the D and G planes, dv is the intersection line between D and V, and dl is the intersection line between the G and V planes (in figure 12, dl is congruent with the point C).
![\includegraphics[width=60mm]{BILDER/realdiam1.eps}](img109.gif) |
![\includegraphics[width=100mm]{BILDER/realdiam2s.eps}](img110.gif) |
For
![]() ,
it is:
,
it is:
| (53) |
| a | = | 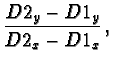 |
(55) |
| c | = | 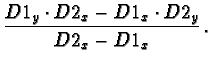 |
(56) |
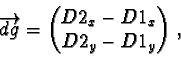
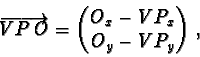
| (57) |
| (58) |
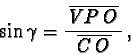 |
(61) |
| = | 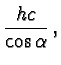 |
(62) | |
| = | 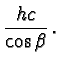 |
(63) |
| (64) |
![\includegraphics[width=60mm]{BILDER/centreangle.eps}](img131.gif) |
They can be obtained with the mapping from the t-frame to the c-space.
In figure 14 it is for a point
P = (Px, Py, Pz):
![]() and
and
![]() (m follows from the lens geometry, equation 7).
(m follows from the lens geometry, equation 7).
For
![]() it is
it is
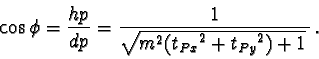 |
(66) |
Finally, the angle ![]() is determined: With VPx and VPy
from equation 59 and 60 and with
equation 7, tVx and tVy can be calculated
and the angle
is determined: With VPx and VPy
from equation 59 and 60 and with
equation 7, tVx and tVy can be calculated
and the angle ![]() is obtained. C is given with the diameter points
D1 and D2, which gives the necessary angle
is obtained. C is given with the diameter points
D1 and D2, which gives the necessary angle ![]() .
.
![\includegraphics[width=60mm]{BILDER/effectcentre.eps}](img137.gif) |
In the situation, where the diameter of the ball is not measured
in the direction, which is vertical to the line co, which goes to
the origin, the centre of the ball
C = (Cx, Cy)
is not simply in the middle of
the visible diameter,
M = (Mx, My) (figure 15):
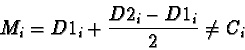 |
(67) |
| = | (68) | ||
| = | 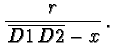 |
(69) |
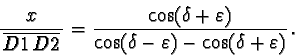 |
(70) |
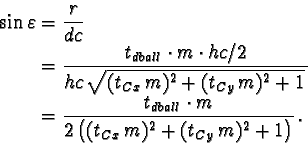 |
(71) |
![\includegraphics[width=105mm]{BILDER/visibility.eps}](img148.gif) |
From a ball, we do not see the real ball diameter 2r, but the
shorter length 2l (figure 16). Instead of
| (72) |
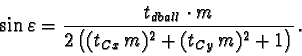 |
(74) |
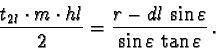 |
(77) |
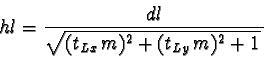 |
(78) |
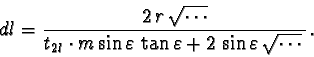 |
(79) |
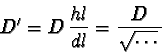 |
(80) |
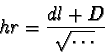 |
(81) |
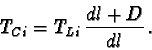 |
(82) |
![\includegraphics[width=80mm]{BILDER/onepicture.eps}](img163.gif) |
At the one picture measurement, the velocity of a ball is measured
within one frame of the video shot. Using a low shutter speed ts,
i.e., values
of 1/200 to 1/30s, the shape of one ball is not distinct but stretched
to a long streak, which is related to the velocity of the ball
(figure 17). The longer the streak, the higher the
velocity of the ball, the larger the streak, the closer is the ball to the
camera. By determining the diameters at the beginning and at the end point
of the ball (B1, B2 and E1, E2 at the ball 3 in the figure), the
locations SB and SE can be calculated, the three-dimensional
velocity
![]() of the ball is given with
of the ball is given with
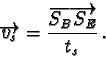 |
(83) |
Since the ball is stretched to a long line, it looses a lot of contrast; it might be very difficult to determine the end points, especially in dense flows, where all the balls have the same color. Using different colors might be very helpful.
In order to get a good resolution of the ball distance, the ball should
be very close to the camera (see figure 1). Assuming
a maximum flow height over ground hmax and a maximum detectable
velocity vmax, it follows for the length of one streak ls
| (84) |
| (85) |
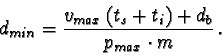 |
(86) |
![\includegraphics[width=53mm]{BILDER/twopicture1.eps}](img171.gif) |
![\includegraphics[width=53mm]{BILDER/twopicture2.eps}](img172.gif) |
Here the velocity of a ball is measured with the time difference ti
from one video shot to the next one (figure 18).
The shutter speed must be set
very high in order to get a distinct shape of the ball
(
![]() s). Beside of this, the
procedure is analogous to the one picture measurement: The location of the
ball is measured in the first frame, with the diameter-points B1 and B2,
and in the next frame, E1 and E2.
s). Beside of this, the
procedure is analogous to the one picture measurement: The location of the
ball is measured in the first frame, with the diameter-points B1 and B2,
and in the next frame, E1 and E2.
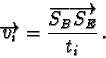 |
(87) |
In addition to the measurement of the velocities, single video frames made with a high shutter speed can be used for the estimation of the ball densities at different heights. Since the balls must not be tracked from one frame to the other one, it is easier to see into the flow and to determine the flow heights of the balls.
The same equations as above are valid, only that the shutter speed ts
has to be replaced with ti, since the balls have to be tracked
during a longer time. It is:
| (88) |
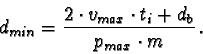 |
(89) |
The accuracy is mostly dependent on the pixel resolution of the video
frame pmax and on the lens characterization. Both informations
are included in the constant m. Let's assume an error of ![]() in pixel or newpixel units (for this calculation the difference can
be neglected) at the measurement of any point in the p-plane.
The error of the middle point of a ball, given from
the end points of the diameter, is
in pixel or newpixel units (for this calculation the difference can
be neglected) at the measurement of any point in the p-plane.
The error of the middle point of a ball, given from
the end points of the diameter, is
![]() .
Related to the diameter, the error is
.
Related to the diameter, the error is
![]() .
From
equation 51 follows the error
.
From
equation 51 follows the error
![]() in the calculation
of the distance hS from the focus of the camera:
in the calculation
of the distance hS from the focus of the camera:
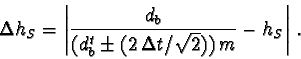 |
(90) |
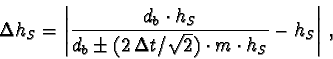 |
(91) |
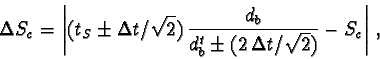 |
(92) |
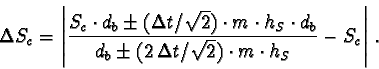 |
(93) |
![\includegraphics[width=72mm]{BILDER/hserror.eps}](img184.gif) |
![\includegraphics[width=72mm]{BILDER/hsscerror.eps}](img185.gif) |
The error
![]() of the horizontal velocity component is
related to the beginning and end point, Bc and Ec, of the vector:
of the horizontal velocity component is
related to the beginning and end point, Bc and Ec, of the vector:
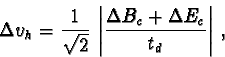 |
(94) |
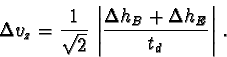 |
(95) |
The estimation of the errors in measuring the coordinates shows very clearly the strong increasing of the inaccuracy with increasing distance from the camera and with increasing distance from the axis of the lens. As a conclusion for the measurement it follows that the balls should be as close to the camera as possible, and balls only situated near the axis of the camera should be used for the evaluation of the position and the velocity.
This work was carried out in the Institute of Low Temperature Science at Hokkaido University in Sapporo/Japan. It took part on the avalanche dynamics project, which includes large and small scale studies on snow flows and ping pong ball flows in the chute of the Shinjo branch of Snow and Ice studies, NIED, Japan, and on the Miyanomori 70m ski jump field in Sapporo. This project includes as well systematic observations of real avalanches in Kurobe Canyon (Japan). I want to express my thanks to Dr. K. Nishimura, who gratefully supported my stay in this institute. This work was enabled by the Japanese Society for the Promotion of Science (JSPS).
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 veval.tex.
The translation was initiated by Jim McElwaine on 1999-10-27