The ping-pong balls avalanche system is a granular flow (the ping-pong balls) interacting strongly with a fluid flow (the air). By strongly interacting we mean that any accurate description must include the force of the air on the balls and the force of the balls on the air.
This system is described by well known equations: The air flow obeys
the Navier-Stokes equations, and each ping-pong ball follows Newtons
law. The force on each ball contains contributions from gravity,
ball-ball forces, ball-ground forces and air-drag forces.
The air-drag force comes from the no-slip boundary condition between
the balls and the air flow. The large range of length and time
scales makes direct integration of the equations of motion very
difficult. Ball-ball collisions occur over time intervals of
order
![]() whereas the duration of the flow is around
whereas the duration of the flow is around
![]() . To resolve the collisions time steps at least ten times
smaller must be used, thus 10 million or so time steps are necessary.
The length scales in the problem are the length of the ski jump
. To resolve the collisions time steps at least ten times
smaller must be used, thus 10 million or so time steps are necessary.
The length scales in the problem are the length of the ski jump
![]() , the length scale given by the volume of the flow
, the length scale given by the volume of the flow ![]() ,
the size of the balls themselves
,
the size of the balls themselves ![]() and the air flow details
around the balls
and the air flow details
around the balls
![]() . A direct integration would require a
grid of size
. A direct integration would require a
grid of size
![]() . Direct
calculations require at least order
. Direct
calculations require at least order ![]() operations and are
obviously infeasible.
operations and are
obviously infeasible.
The most important simplification to make is in the interaction
between the balls and the air. If we consider the air flow only on
a scale much larger than the individual ping-pong balls we can replace
the air-ball no-slip boundary condition by an empirical body force
representing the average drag of the balls on the air. If the grid
squares are taken as ![]() then the total grid size is reduced
to
then the total grid size is reduced
to ![]() and the problem becomes feasible. The volume concentration
of the balls is accounted for as an additional term in the
conservation of mass equation. As a first approximation we regard the
flow as inviscid since the Reynolds number for the flow is of order
and the problem becomes feasible. The volume concentration
of the balls is accounted for as an additional term in the
conservation of mass equation. As a first approximation we regard the
flow as inviscid since the Reynolds number for the flow is of order
![]() (based on the smallest length scale, ball diameter, and ball
terminal velocity) and the drag forces are included explicitly. This
approach fails if there is separation in the flow field. Although the
Reynolds number for the whole flow is of order
(based on the smallest length scale, ball diameter, and ball
terminal velocity) and the drag forces are included explicitly. This
approach fails if there is separation in the flow field. Although the
Reynolds number for the whole flow is of order ![]() , the flow shape
is streamlined and the volume density of the balls is low so
separation may not occur. This is a standard approximation in the
theory of streamlined bodies. Since the Mach numbers in the flow are
low we assume the density of the air is constant. There are no
satisfactory continuum theories for granular flows -- attempts to
extend the kinetic theory of granular matter to dense flows have not
been successful -- so a direct approach is necessary where the
equation of motion for each ball are integrated. This is feasible for
systems of several million balls on current supercomputers.
, the flow shape
is streamlined and the volume density of the balls is low so
separation may not occur. This is a standard approximation in the
theory of streamlined bodies. Since the Mach numbers in the flow are
low we assume the density of the air is constant. There are no
satisfactory continuum theories for granular flows -- attempts to
extend the kinetic theory of granular matter to dense flows have not
been successful -- so a direct approach is necessary where the
equation of motion for each ball are integrated. This is feasible for
systems of several million balls on current supercomputers.
We choose a simple model for ball-ball and ball-ground interactions.
We assume that the normal force ![]() is given by a damped spring and
that the tangential force is given by Coulomb friction. The friction
force is thus
is given by a damped spring and
that the tangential force is given by Coulomb friction. The friction
force is thus ![]() opposing the direction of slip, or
opposing the direction of slip, or ![]() when
there is no slip. This form of friction law is not accurate for long
lasting contacts. A more realistic friction law requires that the
friction can take all values between
when
there is no slip. This form of friction law is not accurate for long
lasting contacts. A more realistic friction law requires that the
friction can take all values between ![]() and
and ![]() depending
on the history of the contact and thus requires extra variables to
describe the history of the contact. During the flow the the volume
densities are low, thus the contact times between balls will be small
so the complexity of accurately modeling static force distributions
is unnecessary for these flows.
depending
on the history of the contact and thus requires extra variables to
describe the history of the contact. During the flow the the volume
densities are low, thus the contact times between balls will be small
so the complexity of accurately modeling static force distributions
is unnecessary for these flows.
We scale the air pressure by the air density and eliminate gravity by
adding a static potential,
![]() , to the
pressure. Since we envisage solving the fluid flow equations over a
scale larger than ball diameter there is no direct coupling between
air pressure changes and air shear rates and the balls. Coupling
between the balls' angular velocity and the air is also neglected. The
direct effect of the static air pressure on the balls is accounted for
by adjusting the gravitational force acting on the balls.
, to the
pressure. Since we envisage solving the fluid flow equations over a
scale larger than ball diameter there is no direct coupling between
air pressure changes and air shear rates and the balls. Coupling
between the balls' angular velocity and the air is also neglected. The
direct effect of the static air pressure on the balls is accounted for
by adjusting the gravitational force acting on the balls.
The system obeys the following equations for conservation of volume, mass and momentum
|
|
volume identity |
|
|
mass conservation |
|
|
air momentum conservation |
|---|---|
|
|
ball |
|
|
ball |
|
|
volume density of air |
|
|
air velocity |
|
|
air pressure |
|
|
position of ball |
|
|
velocity of ball |
|
|
angular velocity of ball |
|
|
volume density of balls |
|
|
total drag |
|---|---|
|
|
drag on ball |
|
|
drag coefficient |
|
|
ball-ball force |
|
|
ball-ground force |
Standard vector calculus notation is used where ![]() denotes the norm
and
denotes the norm
and ![]() a unit vector. Thus for a vector
a unit vector. Thus for a vector ![]()
| (1) | |||
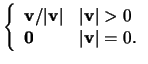 |
(2) |
 |
(3) |
|
|
|
description |
|
|
|
mass |
|
|
|
ball diameter |
|
|
|
ball stiffness |
|
|
|
ball-ball restitution |
|
|
|
ball-ball friction |
|
|
|
ball-ground restitution |
|
|
|
ball-ground friction |
|
|
|
air density |
|
|
|
kinematic air viscosity |
|
|
|
gravity |
|
|
description |
|
|
ball volume |
|
|
ball density |
|
|
buoyancy adjusted gravity |
|---|---|
|
|
ball-ball damping constant |
|
|
ball-ground damping constant |
The equations of motion for the balls are integrated explicitly by
using the leapfrog algorithm. To solve the fluid equations we write
them using the convective derivative
![]() as
as
We have developed a program for DEM (Discrete Element Method) simulations that can handle arbitrary geometries constructed from sections of planes and cylinders, in two or three dimensions and in single or double precision.
The collision detection is normally the most time consuming part of a
DEM simulation. Naive collision detection algorithms take ![]() time. Nearest neighbor schemes using adjacency lists take
time. Nearest neighbor schemes using adjacency lists take ![]() , but with a large scaling constant. Grid schemes, where the balls
are first stored on a grid then adjacent grid squares checked for
collisions, are
, but with a large scaling constant. Grid schemes, where the balls
are first stored on a grid then adjacent grid squares checked for
collisions, are ![]() . However, traditional schemes incur a time and
memory cost proportional to the size of the grid which covers the
whole geometry. For dense granular systems this method is efficient,
but for open systems is impractical -- a grid large enough to cover
the whole ski jump would require
. However, traditional schemes incur a time and
memory cost proportional to the size of the grid which covers the
whole geometry. For dense granular systems this method is efficient,
but for open systems is impractical -- a grid large enough to cover
the whole ski jump would require ![]() of memory. We have
developed a new algorithm where the grid is dynamically resized to
exactly match the extent of the flow. Collisions are detected by
calculating the grid cell for each ball. Then storing the grid
coordinates in the ball list and the ball number in the grid. Next for
each ball the balls in half of the adjacent squares on the grid are
checked for collisions. Once the collisions have been detected the
ball list is then used to clear the grid. The algorithm is thus
of memory. We have
developed a new algorithm where the grid is dynamically resized to
exactly match the extent of the flow. Collisions are detected by
calculating the grid cell for each ball. Then storing the grid
coordinates in the ball list and the ball number in the grid. Next for
each ball the balls in half of the adjacent squares on the grid are
checked for collisions. Once the collisions have been detected the
ball list is then used to clear the grid. The algorithm is thus ![]() per time step independent of the geometry or flow volume.
per time step independent of the geometry or flow volume.
Other contact algorithms have directly searched and cleared the grid.
These algorithms are ![]() , where
, where ![]() is the volume of the grid.
though easier to program and parallelize they are much less efficient
except when the balls are confined to a small volume. In our
algorithm the only cost proportional to
is the volume of the grid.
though easier to program and parallelize they are much less efficient
except when the balls are confined to a small volume. In our
algorithm the only cost proportional to ![]() is the initial clearing
and allocation of the grid, which is only performed once per
simulation.
is the initial clearing
and allocation of the grid, which is only performed once per
simulation.
The balls in the simulation can all be the same, all be different, or
be divided into a small number of classes. The collision detection
algorithm however is inefficient if there is a wide disparity of
ball sizes it scales as
![]() (in 3
dimensions).
(in 3
dimensions).
The program has been tested on single processor systems and can run simulations of the Miyanomori simulations with 10,000 balls in reasonable time -- a few hours to a few days depending on the system. To simulate the large flows the program is designed to run on the University of Hokkaido's Hitachi SR2201. This is a massively parallel supercomputer with 128 active nodes so that simulations with around 10 million balls should be possible. The code has been written, but due to problems with the compiler and operating system it has not yet been tested and debugged.
The air flow equations have not yet been incorporated into the model. In the simulations the air flow is taken to be zero.
The simulations are reasonably accurate for small avalanches (up to 1000 balls), but inaccurate for larger ones. All the simulated flows very rapidly spread out to a thin flow layer less than one ball thick (on average). This then flows down the slope like a solid body expanding or contracting depending on the curvature of the slope. The density is non-uniform indicating some inelastic collapse, but none other of the macroscopic features of the real flow are seen. Fig. 1 shows a six thousand ball simulation.
Though we cannot currently directly simulate the larger flows a two
dimensional flow of ![]() balls will have similarities with a three
dimensional flow of
balls will have similarities with a three
dimensional flow of ![]() balls. Thus we can investigate a
350,000 ball 3 dimensional flow with a 5,000 ball 2 dimensional flow.
These simulations also show very strong damping and rapid spreading.
That is the flows behave like a slowly elongating solid body with
almost no internal motion. This is not surprising. Without
interaction with a non-constant air flow there are only very weak
mechanisms to generate internal motion and any internal motion is
rapidly damped, even when the restitution coefficients are close to
one.
balls. Thus we can investigate a
350,000 ball 3 dimensional flow with a 5,000 ball 2 dimensional flow.
These simulations also show very strong damping and rapid spreading.
That is the flows behave like a slowly elongating solid body with
almost no internal motion. This is not surprising. Without
interaction with a non-constant air flow there are only very weak
mechanisms to generate internal motion and any internal motion is
rapidly damped, even when the restitution coefficients are close to
one.
We can also run the simulation with an increased ball size so as to represent a larger number of balls. Figure 2 shows a simulation with one thousand balls where the ball radius is increased by a factor of seven so that each ball has the volume of 350 real ping pong balls. Thus the whole flow has the volume of a 350,000 ball flow. Results from simulations with altered radii cannot be compared with the data but they make it much easier to see the individual motion of the balls.
The large flows attain mean speeds of more than five times the speed of a single ball on the slope. They achieve such speeds because of the acceleration of the air, so it is no surprise that the current simulations assuming zero air velocity are incorrect. The failure of the incomplete model supports our physical intuition that the air flow dynamics are crucial to understanding the ping-pong ball flows. We hope to complete the model with the air flow over the coming year.
The accelerating force on the flow is simple and due only to gravity
![]() , where
, where ![]() is the slope angle. Henceforth we
will drop the superscript
is the slope angle. Henceforth we
will drop the superscript ![]() on
on ![]() but always mean the buoyancy
adjusted gravity.
but always mean the buoyancy
adjusted gravity.
There are three main processes which will cause apparent drag between the balls and the slope.
When a ball's linear velocity does not match its angular velocity
there is slip between the ball and the surface and there is a
resistive force of magnitude
![]() in the direction
opposing the relative motion. Since the balls are shells and the
collisions are totally inelastic each time they collide with the
ground, assuming no initial rotation, they lose half their downslope
velocity before slipping stops. However, each ball only hits the
ground at most once, since the inelastic nature of the ground make it
impossible for rolling balls to become airborne (unless there are very
high air velocities.) To calculate the effect of this force we need to
know the rate of collisions. A reasonable approximation is that the rate
is constant per distance traveled. Then the rate of impacts is
in the direction
opposing the relative motion. Since the balls are shells and the
collisions are totally inelastic each time they collide with the
ground, assuming no initial rotation, they lose half their downslope
velocity before slipping stops. However, each ball only hits the
ground at most once, since the inelastic nature of the ground make it
impossible for rolling balls to become airborne (unless there are very
high air velocities.) To calculate the effect of this force we need to
know the rate of collisions. A reasonable approximation is that the rate
is constant per distance traveled. Then the rate of impacts is
![]() , where
, where ![]() is the length of the slope. Then the
resistive force due to Coulomb friction is
is the length of the slope. Then the
resistive force due to Coulomb friction is
For balls rolling along the ground there is no Coulomb frictional
drag, but instead drag caused by collisions with surface roughness.
If we imagine this roughness as being composed of obstacles height ![]() ,
spacing
,
spacing ![]() , the balls will hit obstacles at a rate of
, the balls will hit obstacles at a rate of ![]() and
receive an impulse of
and
receive an impulse of
![]() , where
, where
![]() . in the usual case, when
. in the usual case, when ![]() , the total
resistive force is
, the total
resistive force is
![]() . Thus this drag
force is linear in velocity.
. Thus this drag
force is linear in velocity.
The final force is due to the special structure of the ski jump. It is
made from overlapping layers of bristles. Where the bristles overlap
the next layer there is a drop. The balls rolling down the slope thus
free-fall briefly as they roll over the lip and then dissipate energy
in the inelastic collision with the ground. If ![]() is the angle of
the flat sections then this produce a resistive force of
is the angle of
the flat sections then this produce a resistive force of
![]() .
.
All three of these ground drag forces are small compared to ![]() in
the middle of the slope and in the first order analysis we present
here they are all neglected. This approach is supported by the data
since the velocity profile for the balls is flat -- ball velocities
are not lower near the ground.
in
the middle of the slope and in the first order analysis we present
here they are all neglected. This approach is supported by the data
since the velocity profile for the balls is flat -- ball velocities
are not lower near the ground.
The Reynolds number for the flow if of the order ![]() (based on flow
height
(based on flow
height ![]() velocity
velocity
![]() ). Since the flow
is reasonably streamlined and porous we can assume that separation
does not occur and ignore viscosity. The air drag force can then only
depend on the air density, front velocity and the length scale. The
only combination of these with the correct dimensions is
). Since the flow
is reasonably streamlined and porous we can assume that separation
does not occur and ignore viscosity. The air drag force can then only
depend on the air density, front velocity and the length scale. The
only combination of these with the correct dimensions is ![]() . The implicit assumptions here are that the air flow is in an
equilibrium state in the frame of reference moving with the flow. And
that the pressure variation due to the slowly changing nature of the
flow are small. These assumptions are widely made when considering air
drag on objects and will result only in small errors. The biggest
source of error here comes from only using one length scale. At the
start of the flow the length scale of the box will be important, and
at the end of the flow the length scale of the individual balls will
be important. In fact any flow on a long enough slope will eventually
be reduced to a single thickness flow so needs at least two length
scales to describe it. These additional length scales could also be
regarded as dimensionless parameters (Scaling
. The implicit assumptions here are that the air flow is in an
equilibrium state in the frame of reference moving with the flow. And
that the pressure variation due to the slowly changing nature of the
flow are small. These assumptions are widely made when considering air
drag on objects and will result only in small errors. The biggest
source of error here comes from only using one length scale. At the
start of the flow the length scale of the box will be important, and
at the end of the flow the length scale of the individual balls will
be important. In fact any flow on a long enough slope will eventually
be reduced to a single thickness flow so needs at least two length
scales to describe it. These additional length scales could also be
regarded as dimensionless parameters (Scaling ![]() to get a length)
that describe the shape of the flow. In fact by including an arbitrary
number of these parameters one can obtain approximations of any degree
to the shallow water equations. To first order, a little after the
flows have left the box, and before the flows become degenerate we can
hope that one length scale is a reasonable approximation.
to get a length)
that describe the shape of the flow. In fact by including an arbitrary
number of these parameters one can obtain approximations of any degree
to the shallow water equations. To first order, a little after the
flows have left the box, and before the flows become degenerate we can
hope that one length scale is a reasonable approximation.
The equation of motion for the front of the flow is thus
Non-dimensional parameters that have been excluded are the Froude
number
![]() , the relative density
, the relative density
![]() and the length scale ratio
and the length scale ratio ![]() . The Froude number
represents the gravitational spreading of the flow and is important
initially for the flow out of the box. The relative density is a
measure of the porosity of the flow (the amount of air in the flow)
and will effect the drag coefficient (absorbed into the length scale
in the equation). We show that scaling the equations with respect to
leaves these parameters unaffected and partly explains the excellent
agreement of the data with the scaling laws. The last parameter, the
length scale ratio, will only be important for flows as they spread
out to one ball thick and can be ignored for large flows at
Miyanomori.
. The Froude number
represents the gravitational spreading of the flow and is important
initially for the flow out of the box. The relative density is a
measure of the porosity of the flow (the amount of air in the flow)
and will effect the drag coefficient (absorbed into the length scale
in the equation). We show that scaling the equations with respect to
leaves these parameters unaffected and partly explains the excellent
agreement of the data with the scaling laws. The last parameter, the
length scale ratio, will only be important for flows as they spread
out to one ball thick and can be ignored for large flows at
Miyanomori.
The length scale of the flow will also obey a differential equation
depending on the Froude number
Now we consider the equations applied to flows of ![]() balls. The mass
of the flow
balls. The mass
of the flow ![]() and we define a dimensionless function
and we define a dimensionless function ![]() such that
such that
![]() .
. ![]() will be of order 1 and
independent of
will be of order 1 and
independent of ![]() for non-degenerate flows. Equation
for non-degenerate flows. Equation ![]() is
then
is
then
The success of this simple analysis is partly explained by the
independence on ![]() of the relative density,
of the relative density,
The data for front positions and velocities are limited and contains
large errors so, at present, the data are too limited to quantatively
analyze the length scale change functions ![]() and
and ![]() .
However, fig
.
However, fig ![]() shows that after the initial surge it is at
least plausible that
shows that after the initial surge it is at
least plausible that ![]() is the same, roughly constant, function
for both flows.
is the same, roughly constant, function
for both flows.
This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -image_type gif -split 0 miya_similarity.tex
The translation was initiated by Jim McElwaine on 2000-11-14