SIZE SEGREGATION IN SNOW AVALANCHES
Observations and Experiments
| J. MCELWAINE and K. NISHIMURA |
| Institute of Low Temperature Science, Hokkaido University |
|---|
| Kita-19, Nishi-8, Kita-ku, Sapporo, JAPAN 060 |
|---|
In general, well-developed dry snow avalanches consist of at least two
stratified layers: snow cloud at the top and dense flowing snow at the
bottom [1]. It is well known that the snow cloud sometimes travels faster
and farther than the flowing part and may cause serious damage in the runout
area. However, since the dense flow often involves most of the mass of the
avalanche and is very destructive, understanding its characteristics is of
practical significance.
In order to increase our knowledge of avalanche dynamics and to contribute
to avalanche zoning and to the design of protection structures, we have
carried out natural snow avalanche observations (Shiai Valley, Japan and
Ryggfonn, Norway) and also experiments at a ski-jump. In this paper we
briefly introduce both approaches and also preliminary results of size
segregation experiments.
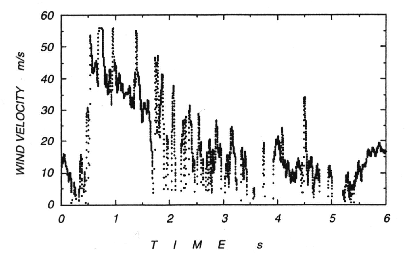
Figure 1:
Air velocities in a snow cloud calculated with the recordings of
the static pressure depression at the Shiai Valley on January 29
1996.
|
|
In the Shiai Valley, a systematic investigation of natural powder snow
avalanche has been under way since 1989. In winter, snow usually
accumulates to more than 20 m in the valley and the air temperature
falls to below
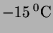 [2]. Shiai Valley runs from an
elevation of 1600 m (a.s.l.) to the Kurobe River at an elevation of
600m; its length is about 2000 m, the vertical drop is 1000 m and the
average angle of inclination is
[2]. Shiai Valley runs from an
elevation of 1600 m (a.s.l.) to the Kurobe River at an elevation of
600m; its length is about 2000 m, the vertical drop is 1000 m and the
average angle of inclination is 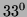 . At the main observation site,
at the midpoint of the avalanche path, instruments were set to measure
avalanche impact pressures, wind velocity, wind pressure, atmospheric
pressure, temperature and ground vibration. Avalanche movement was
recorded with three video cameras. Most of the equipment was installed
on two steel mounts of cylinders 0.3 m in diameter and 5 m in height.
Data were recorded at a rate of 1 kHz by the data acquisition system
in an underground room. Detailed information on the measurement system
can be found in Kawada et al.[2] and Nishimura et al.[3].
. At the main observation site,
at the midpoint of the avalanche path, instruments were set to measure
avalanche impact pressures, wind velocity, wind pressure, atmospheric
pressure, temperature and ground vibration. Avalanche movement was
recorded with three video cameras. Most of the equipment was installed
on two steel mounts of cylinders 0.3 m in diameter and 5 m in height.
Data were recorded at a rate of 1 kHz by the data acquisition system
in an underground room. Detailed information on the measurement system
can be found in Kawada et al.[2] and Nishimura et al.[3].
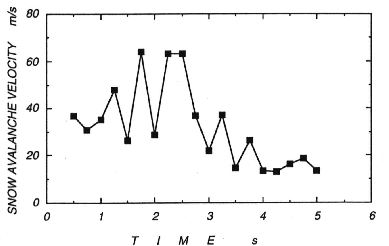
Figure 2:
Velocities of the lower flowing layer of the avalanche calculated
by correlating the data from the impact pressure sensors at the
Shiai Valley on January 29 1996.
|
|
Figure 1 shows the air velocities calculated from the
static pressure difference between in an avalanche cloud and in the
underground room during the passage of a dry snow avalanche on January
29, 1996. Since the snow cover was observed to be about 2 m deep, it
presents the recording at around 3 m above the snow surface. It was
the largest avalanche in seven years, and was strong enough to damage
the observation tower and to destroy some instruments. The velocity of
the snow cloud showed a rapid increase to more than 56 m/s, the limit
of measurement with this system. The velocity then declined gradually
with periodic fluctuations.
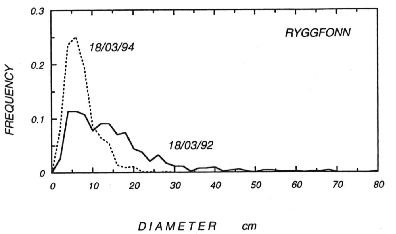
Figure 3:
Size distribution of snow blocks observed in avalanche debris in
Ryggfonn, Norway. One on March 18, 1994 was a dry snow avalanche
and the other one, released on March 18, 1992, was a wet one.
|
|
Velocities of the lower flowing layer were also calculated by
correlating the data from the impact pressure sensors. The
cross-correlation function was calculated at 0.25 s intervals from a
time series of impact data to find the average internal snow flow
velocity. The velocity was obtained every 0.25 s from a combination of
the lag time that gave the highest correlation and the distance
between the two measuring points. Further details of the method have
been given in Nishimura et al. [3]. Calculated velocities are
presented in Figure 2 which shows that the magnitude and the
variation of the velocity in the snow cloud are in approximate
agreement with the velocity of the dense layer, which suggests a close
interaction between the two. Since the interval of calculation here is
much coarser than the sampling rate of static pressure depression
(
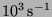 ), we cannot compare the data directly. However, it
is noteworthy, that the velocities of the snow flow also show a
periodic change with a dominant frequency of around 1 Hz [5]. Such
longitudinal wave-like characteristics were also found by McClung and
Schaerer (1985) for both wet and dry avalanches.
), we cannot compare the data directly. However, it
is noteworthy, that the velocities of the snow flow also show a
periodic change with a dominant frequency of around 1 Hz [5]. Such
longitudinal wave-like characteristics were also found by McClung and
Schaerer (1985) for both wet and dry avalanches.
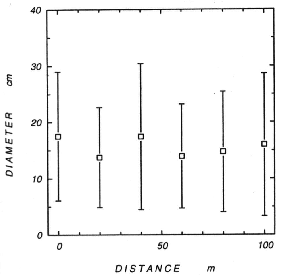
Figure 4:
Size distribution of snow blocks along the avalanche path measured
in Ryggfonn, Norway on March 18, 1992. Zero on the horizontal
axis corresponds to the front of the avalanche debris.
|
|
Although precise data are very difficult to obtain, it is known that
the flowing layers are usually composed of fluidized snow and a number
of snow blocks. Figure 3 shows the size distribution of snow
blocks observed in avalanche debris in Ryggfonn, Norway both of which
were released with an explosion at 1530 m (a.s.l.) and ran down 1600 m
on an avalanche path of 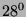 mean slope [6-7]. One on March 18,
1994 was a dry snow avalanche and the other one, released on March 18,
1992, was a wet one. In Figure 3 we see the wet one has a
wide size distribution and is larger in average (16.0 cm) than the dry
one (8.3 cm). In the latter case we also measured the size
distribution of snow blocks along the avalanche path every 20m (see
Figure 4); zero on the horizontal axis corresponds to the
front of the avalanche debris. Although it has been reported in the
debris flow that the bigger rocks tend to appear near the front due to
segregation processes [8], the snow avalanche in Figure 4
shows a rather uniform distribution.
mean slope [6-7]. One on March 18,
1994 was a dry snow avalanche and the other one, released on March 18,
1992, was a wet one. In Figure 3 we see the wet one has a
wide size distribution and is larger in average (16.0 cm) than the dry
one (8.3 cm). In the latter case we also measured the size
distribution of snow blocks along the avalanche path every 20m (see
Figure 4); zero on the horizontal axis corresponds to the
front of the avalanche debris. Although it has been reported in the
debris flow that the bigger rocks tend to appear near the front due to
segregation processes [8], the snow avalanche in Figure 4
shows a rather uniform distribution.
However, Issler et al. [9] observed that the larger snow blocks
existed nearer the surface than the smaller ones by the pit
observations of snow avalanche debris. Thus size segregation seem to
happen in snow avalanches as well.
In addition it should be also noted that avalanche balloons have
been developed as a safety device that can reduce the risk of
avalanche burial and are already in practical use. In case of an
avalanche, the skier triggers the balloon, which is folded and carried
in a specially designed backpack, by releasing pressurized gas from a
cartridge. It helps to prevent the victims being buried by increasing
his volume. The victim rises through the surrounding smaller snow
blocks and particles to the surface of the layer, where, due to the
higher velocity at the surface, they move on to the front of the
avalanche. Static buoyancy alone cannot explain the effect of the
avalanche balloon, since flow densities are typically less than 400
kg/m3 which is about the density of the victim with the inflated
balloon. Tschirky and Schweizer[10] carried out the field test and
proved its efficiency.
Figure 5:
550,000 ping-pong ball flow along the ski jump.
|
|
Perhaps it is right to say that snow avalanches are made up of
granular materials. After a dry snow avalanche starts, the snow blocks
are broken into smaller lumps or even ice particles. On the other
hand, after a wet snow avalanche stops we find a number of snow balls
in the debris as shown in Figure 3. Hence, some of the
results from studying granular flows can be applied to snow avalanche
modeling [11], but unfortunately most of the theories and numerical
simulations developed so far appear too simplified to realistically
describe the snow avalanches. To investigate granular flows, we
carried out inclined chute experiments with snow and ice spheres in a
cold laboratory and obtained the profiles of density and velocity as
functions of inclination and temperature [12]. However, it was unclear
whether the flow reached the steady-state in the 5.4 m long chute.
Thus, as a next step, we have started avalanche experiments on the
Miyanomori ski jump in Sapporo, because it offers the longest inclined
plane under controlled conditions. In winter, natural snow (300 kg
maximum) was used. In summer, on the other hand, we have released up
to 550,000 ping-pong balls to perform three dimensional granular
experiments [13].
The ping-pong balls used in this study were 37.7 mm in diameter and
weighted 2.48 g. Since the effect of the air drag acting on such a
light ball is fairly large, the flow velocities were expected to
arrive at steady state within a short distance. In fact, Nohguchi et
al. [14] found in their 22 m long chute experiments that the front
velocity of ping-pong ball flow became nearly constant at 10m
downstream of the starting point. Furthermore, they concluded with
their similarity analysis that the ping-pong flow on the 100 m long
slope corresponded to the natural powder snow avalanches which run
down for a few kilometer distance [13,14].
In the experiments, up to 500,000 ping-pong balls were stored in a
large container set on top of the landing slope. They were released
simultaneously by opening the gate of the container. The flow
accelerated down along the 150m long and 30 m wide slope, the floor of
which was made with an artificial grass and its inclination amounted
to 36 deg. from K to P point. The individual movements of the balls
and the behavior of the flow were recorded with several video cameras
(Figure 5).
Figure 6:
Leading edge velocity of the ping-pong ball flow.
|
|
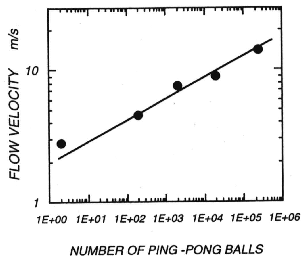
Figure 6 shows the leading edge velocity as a function of
runout distance when 250,000 ping-pong balls were released from 15 m
down the top. The flow accelerated linearly with the distance down the
inclined artificial grass floor and its velocity eventually amounted
to 15 m/s 65 m down from the starting point. Then the flow kept the
velocity almost constant for 30m until the inclination started to
decrease; that is a steady granular flow moving at its inherent
terminal velocity was obtained. The flow spread out laterally and
longitudinally as it moved down the slope (Figure 5) and,
after passing the steepest part, the flow came to a stop on the
braking track.
Figure 7:
Leading edge velocities from K to P point as a function of
released ball numbers. The line was derived theoretically by
Nohguchi et al. (1996).
|
|
The flow velocities and run out distance strongly depended on the
number of released balls. The leading edge velocities measured from K
to P point are given in Figure 7 as a function of the number
of released balls. The velocity showed a remarkable growth from 2.8 to
15 m/s as the number of ping-pong balls increased from 2 to 300,000.
Generally not only air drag but also particle-particle and
particle-floor collision act to reduce the velocity. In fact, when two
balls were released the velocity was only 2.8 m/s; each ball ran down
individually without interaction. This velocity is much less than the
free fall velocity of a ping-pong ball, which is
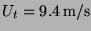 . However, with an increasing numbers of balls the
free fall velocity was reached and surpassed. In fact the largest
velocity was 15 m/s which is 1.5 times larger than the free fall
velocity.
. However, with an increasing numbers of balls the
free fall velocity was reached and surpassed. In fact the largest
velocity was 15 m/s which is 1.5 times larger than the free fall
velocity.
In the experiments, as the number of balls increased, the head and
tail structure became clearer and clearer. When 250,000 balls were
released, the thickness of the head was higher than 60 cm which
corresponds to about 16 particles diameters. Although the individual
balls changed positions rapidly, the leading edge flowed like a
consolidated body. Hence, it is reasonable to say that the size of the
head gives a strong effect on the flow velocity change listed in
Figure 7.
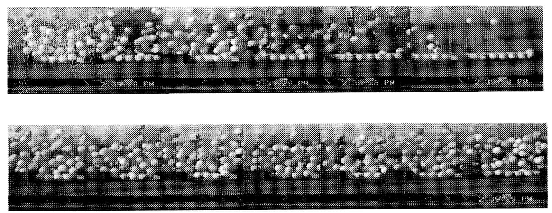
Figure 9:
Ping-pong flow along the chute of the Shinjo Branch of Snow and
Ice Studies, NIED. The flow consists of larger balls (44 mm in
diameter and 2.2 g in weight) and ordinary ones (38 mm in
diameter and 2.5 g in weight).
|
|
In addition to the velocity and particle concentration measurements
described above, we have put some particles (balls) with different
size and densities from the ping-pong balls in the container in order
to look at the segregation process in the flow. Although more
experiments and careful analysis will be necessary, it might be noted
that a plastic ball, the diameter of which is about twice that of
ping-pong ball (6.8 cm in diameter) and the density of which is
comparable (18.1 g in weight), appeared at the front part of the
debris (Figure 8). Further, aiming at investigating
segregation process in granular flows along the chute, we have also
carried out the ping-pong flow experiments in the chute of the Shinjo
Branch of Snow and Ice Studies, NIED, Japan. The chute has a slope
angle of 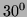 and a width of 1 m. One side of the wall consists of
glass plate, while the other side is made of wood. Larger ping-pong
balls, 44 mm in diameter and 2.2 g in weight are used as well as
ordinary ones. All the balls were kept in a container at the top of
the chute and released simultaneously. Before each run the
ping-pong balls are spread all over the floor to make a rough and
uniform surface. Figure 9 shows the flow situation. At this
stage no clear findings have been obtained, but we expect that the
combination of the above experiments and the simulation of
3-dimensional, inhomogeneous two-phase flows, will make it possible
to reveal the segregation process in avalanche flows.
and a width of 1 m. One side of the wall consists of
glass plate, while the other side is made of wood. Larger ping-pong
balls, 44 mm in diameter and 2.2 g in weight are used as well as
ordinary ones. All the balls were kept in a container at the top of
the chute and released simultaneously. Before each run the
ping-pong balls are spread all over the floor to make a rough and
uniform surface. Figure 9 shows the flow situation. At this
stage no clear findings have been obtained, but we expect that the
combination of the above experiments and the simulation of
3-dimensional, inhomogeneous two-phase flows, will make it possible
to reveal the segregation process in avalanche flows.
The authors gratefully acknowledge all our colleagues who joined our
measurements at Shiai Valley and experiments at the ski jump. It is
certain the work could not have been completed without their
cooperation. These projects were partly supported by Grant-in-Aid for
Co-operative Research from the Science Research of the Ministry of
education, Science and Culture, Japan.
- 1.
- Schaerer, P. A., Friction coefficient and speed of flowing
avalanches. International Association of Hydrological
Sciences Publication 114 (Symposium at Grindelwald 1974
-- Snow Mechanics), 425-432, 1975.
- 2.
- Kawada, K., K. Nishimura, and N. Maeno, 1989. Experimental
studies on a powder snow avalanche, Annals of Glaciology,
13, 129-134.
- 3.
- Nishimura, K., H. Narita, N. Maeno, and K. Kawada, 1989. The
internal structure of powder-snow avalanches, Annals of
Glaciology, 13, 207-210.
- 4.
- Nishimura, K. and Y. Ito, 1997. Velocity distribution in snow
avalanches. Journal of Geophysical Research, Vol. 102, No.
B12, 27297-27303.
- 5.
- McClung, D. M. and P. A. Schaerer, 1985. Characteristics of
flowing snow and avalanche impact pressures, Annals of
Glaciology, 6, 9-14.
- 6.
- Nishimura, K., N. Maeno, F. Sandersen, K. Kristensen, H. Norem,
and K. Lied, 1993. Observations of the dynamic structure of snow
avalanches, Annals of Glaciology, 18, 313-316.
- 7.
- Nishimura, K., F. Sandersen, K. Kristensen, and K. Lied, 1995.
Measurements of powder snow avalanche -Nature-, Surveys in
Geophysics, 16, 649-660.
- 8.
- Curry, R. R., 1966. Observation of Alpine mud-flows in the Tenmile
range, Central Colorado, Bull. Geol. Soc. Am., Vol. 77, 771-776.
- 9.
- Issler, D., P. Gauer, M. Schaer and S. Keller, 1996.
Staublawinenereignisse im Winter 1995: Seewis, Adelboden und Col du
Pillon, Interner Bericht Nr. 694.
- 10.
- Tschirky, F and J. Schweizer, Avalanche balloons -preliminary
test results, Proceedings of the International Snow Science
Workshop, 1996 in Banff, 309-312, 1997.
- 11.
- Savage, S. B., 1983. The flow of granular materials,
Chemical Engineering Science, Vol. 38, No.2, 189-195,
1983.
- 12.
- Nishimura, K., K. Kosugi, and M. Nakagawa, 1993. Experiments on
ice-sphere flows along an inclined chute, Mechanics of
Materials, 16, 205-209.
- 13.
- Nishimura, K., S. Keller, J. McElwaine and Y. Nohguchi, 1998.
Ping-pong ball avalanche at a ski jump, Granular Matter,
Vol. 1, 51-56.
- 14.
- Nohguchi, Y., K. Nishimura, T. Kobayashi, K. Iwanami, K.
Kawashima, Y. Yamada, H. Nakamura, K. Kosugi, O. Abe, A. Sato, Y.
Endo, Y. Kominami, and K. Izumi, 1996. Similarity of avalanche
experiments by light particles, Proceedings of INTERPRAVENT
1996 -Garmisch-Partenkirchen, Tagungspublikation, Band 2,
147-156.
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -image_type gif -notransparent segregation
The translation was initiated by Jim McElwaine on 2000-11-14



Jim McElwaine
2000-11-14